[백준] 2133 타일 채우기 (Java)

2133번: 타일 채우기

문제

3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.

 

입력

첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.

 

출력

첫째 줄에 경우의 수를 출력한다.

 

 

---

접근 방식

접근

1 ≤ N ≤ 30 이므로, 3x1부터 3x30 타일에 대한 경우의 수를 arr 배열에 저장하고, arr[N] 값을 출력한다.

부분 문제를 해결하기 위하여 점화식을 세워보자.

우선, arr[0]=1 이고, 홀수인 i에 대해서는 경우의 수가 모두 0이다.

 

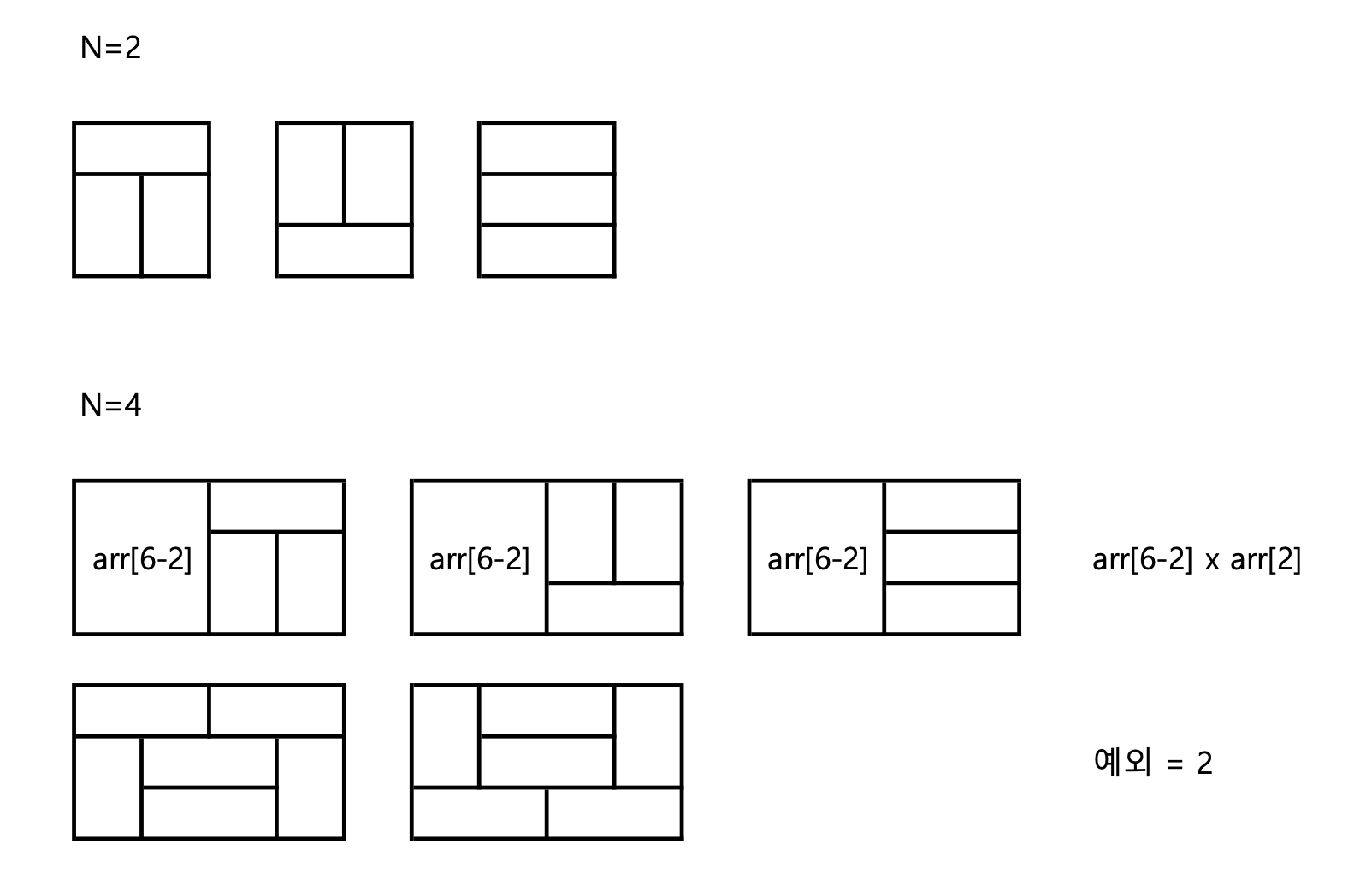
1. i=2

3x2 타일에 대하여 3가지 경우의 수가 존재한다.

 

2. i=4

    a. 3x4 는 3x2 옆에 3x2 타일을 붙인다고 생각할 수 있다. 따라서, arr[4] = arr[4-2] * arr[2]를 작성할 수 있다.

    b. 그런데, i 가 4 이상(짝수)일 때, 매번 가장자리의 두 2x1 타일 사이에 1x2 타일들을 배치하는 예외가 2개씩 발생한다.

 

따라서, i=4일 때는 최종적으로 arr[4] = arr[2] * arr[2] + 2가 된다.

 

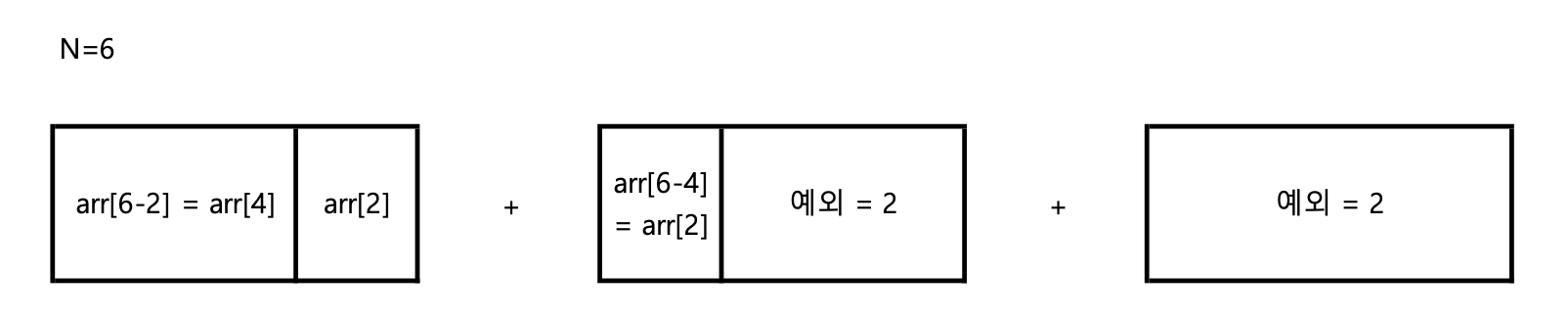
3. i=6

    a. 3x6 도 3x4 옆에 3x2 타일을 붙이는 것을 가장 먼저 생각할 수 있다. 따라서, arr[6] = arr[6-2] * arr[2] 가 된다.

    b. arr[6]은 i=4 였을 때 발생했던 두 가지 예외 옆에 붙는 타일에 대한 경우의 수도 포함해야한다. 이 때 남은 길이 2(6-4)에 대하여 3x2 타일에 대한 경우의 수는 arr[6-4] 이므로, 2 * arr[2]이다.

    c. i=6일 때 또한 새로운 예외 2개가 생긴다.

 

따라서, i=6일 때는 최종적으로 arr[6] = arr[4] * arr[2] + arr[2] * 2 + 2 가 된다.

 

알고리즘

점화식

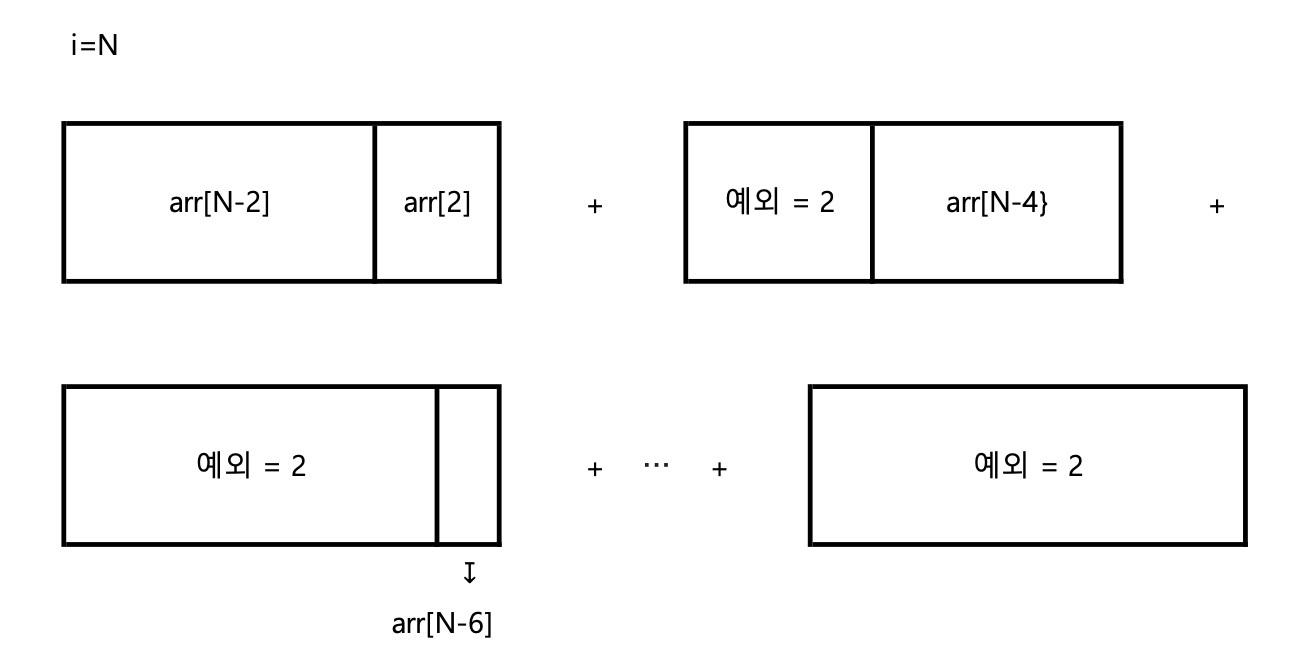
i=N (N>=4)

1. 3x(N-2) 옆에 3x2 타일을 붙이는 경우의 수
   • = arr[N-2] * arr[2]
2. i=4, 6, ..., N-2 일 때 발생했던 두 가지씩의 예외 옆에 붙는 타일에 대한 경우의 수
   • arr[N-4] * 2 + arr[N-6] * 2 + ... + arr[N-(N-2)] * 2
   • -> i=4, 6, ..., N-2 새로 추가되는 예외 타일 2가지씩에 대한 경우의 수를 모두 합함
3. i=N일 때 생기는 새로운 예외 2개: arr[N-N] * 2, 즉, arr[0] * 2 로 나타낼 수 있음
   • arr[i] = arr[i-2] * arr[2] + arr[i-4] * 2 + arr[i-6] * 2 + ... + arr[2] * 2 + arr[0] * 2

 

 

시간 복잡도

이중 for문 -> O(N^2)

 

 

---

Code

코드를 보기 전에 스스로 구현해 보는 것을 권장합니다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class BJ_2133 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());

        int[] arr = new int[31];
        arr[0] = 1;
        arr[2] = 3;

        for(int i=4; i<31; i++) {
            arr[i] = arr[i-2] * arr[2];
            for(int j=4; j<=i; j++){
                arr[i] += arr[i-j]*2;
                j++;
            }
            i++;
        }

        System.out.print(arr[N]);
    }
}