| 본 글은 건국대학교 알고리즘 동아리 AlKon 스터디 5조에서 진행된 발표 내용입니다. |
11060 점프 점프
11060번: 점프 점프
재환이가 1×N 크기의 미로에 갇혀있다. 미로는 1×1 크기의 칸으로 이루어져 있고, 각 칸에는 정수가 하나 쓰여 있다. i번째 칸에 쓰여 있는 수를 Ai라고 했을 때, 재환이는 Ai이하만큼 오른쪽으로
www.acmicpc.net
| 시간 제한 | 입력 | 범위 |
| 1초 | N, A(N개의 수) | 1 ≤ N ≤ 1000 // 1 ≤ A ≤ 100 |
1xN 크기의 배열에서, i 번째 칸에 적힌 수를 Ai 라고 할 때, 해당 칸에서 오른쪽으로 Ai칸 이하만큼 점프할 수 있다.
가장 왼쪽 끝에서 오른쪽 끝으로 갈 때, 점프 횟수의 최솟값을 구하여라.
접근법
점프 횟수의 최솟값을 구해야 하므로, dp 배열의 모든 값은 MAX(1001)로 초기화한다. 단, dp[0]은 처음부터 접근하므로 값이 0이다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| arr | 1 | 2 | 0 | 1 | 3 | 2 | 1 | 5 | 4 | 2 |
| dp | 0 | MAX | MAX | MAX | MAX | MAX | MAX | MAX | MAX | MAX |
현재 위치에서 갈 수 있는 모든 칸에 대하여 최적의 값을 계산을 하면 된다.
index를 i라고 하자.
1. i=0 → arr[i]=1 이므로, 1번 칸까지 갈 수 있다.
비교해야 하는 값: 기존 dp[i+1] 값 vs dp[i] + 1 : MAX vs 0+1 → 1이 더 작으므로, dp[1] = dp[0] + 1로 갱신
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| arr | 1 | 2 | 0 | 1 | 3 | 2 | 1 | 5 | 4 | 2 |
| dp | 0 | 1 | MAX | MAX | MAX | MAX | MAX | MAX | MAX | MAX |
2. i=1~4 (생략)
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| arr | 1 | 2 | 0 | 1 | 3 | 2 | 1 | 5 | 4 | 2 |
| dp | 0 | 1 | 2 | 2 | 3 | 4 | 4 | 4 | MAX | MAX |
3. i=5 → arr[i]=2 이므로, 7번 칸까지 갈 수 있다.
a. dp[6] vs dp[5]+1 = 4 vs 4+1 → 4가 더 작으므로, dp[6] = dp[6] 유지
b. dp[7] vs dp[5]+1 = 4 vs 5+1 → 4가 더 작으므로, dp[6] = dp[6] 유지
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| arr | 1 | 2 | 0 | 1 | 3 | 2 | 1 | 5 | 4 | 2 |
| dp | 0 | 1 | 2 | 2 | 3 | 4 | 4 | 4 | MAX | MAX |
4. i=6~9 (생략)
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| arr | 1 | 2 | 0 | 1 | 3 | 2 | 1 | 5 | 4 | 2 |
| dp | 0 | 1 | 2 | 2 | 3 | 4 | 4 | 4 | 5 | 5 |
기존 dp[i+j] 값과 dp[i] + 1 값을 비교해야 하는 이유 ( j ≤ arr[i] )
엥.? 내가 i에 위치해 있을 때, 기존 dp[i+j]은 전부 MAX 아니야? 라고 생각할 수 있다.
하지만, 위 3번에 붉은 글씨의 열(i=4)을 보자.
이 칸에서는 최대 3칸까지 점프가 가능하기 때문에, dp[5]~dp[7]의 값이 모두 4로 갱신된다.
따라서, i=5가 되었을 때 dp[6]과 dp[7]의 값이 MAX가 아니다.
이때, dp[6]과 dp[7]은 dp[i+j]에 해당한다. ( dp[6] = dp[i+1], dp[7] = dp[i+2] )
이는 즉, 현재 위치에서 점프하기 전에 앞의 다른 어떤 칸에서 이미 점프한 경우 또한 고려가 가능하다는 것을 의미한다.
두 경우 중 어느 방법의 점프 횟수가 적은 지는 이 때, 다시 판단한다.
알고리즘
- 입력 가능한 칸의 수를 arr 배열에 저장한다.
- 동시에 dp 배열은 MAX로 초기화한다. (MAX = 1001)
- 각 칸에서 갈 수 있는 칸들에 대하여, 점프 횟수의 최솟값을 갱신한다.
- 현재 칸에서 한 번 이동하는 횟수 (현재 칸 dp 값 + 1)
- 원래 각 칸에 저장되어 있던 값 (MAX 혹은 앞 과정에서 갱신된 dp[i + j] 값)
- a와 b를 비교하여 더 작은 값을 dp[i + j]에 저장한다.
- 최소 몇 번 점프를 해야 가장 오른쪽 끝 칸으로 갈 수 있는지 출력한다.
- 점프를 통해 가장 오른쪽으로 갈 수 없는 경우, -1을 출력
- : dp[n-1] == MAX; 갱신되지 않음 = 도달한 적이 없음
시간복잡도
최악의 경우
i가 0부터 n-1까지 탐색할 때, 모든 j가 1부터 n-i-1까지 탐색
(N-1) + (N-2) + (N-3) + … + (N-(N-2)) + (N-(N-1))
→ O(N^2)
제출
틀렸습니다 → 맞았습니다!!
#define MAX101 → 1001
Code - C++
코드를 보기 전에 스스로 구현해 보는 것을 권장합니다.
#include <iostream>
#include <vector>
#include <algorithm>
#define MAX 1001
using namespace std;
int main(){
int n;
cin >> n;
vector<int> vt(n), dp(n);
for(int i=0; i<n; i++) {
cin >> vt[i];
dp[i] = MAX;
}
dp[0] = 0;
for(int i=0; i<n; i++){
for(int j=1; j<=vt[i] && i+j<n; j++){
dp[i+j] = min(dp[i] + 1, dp[i+j]);
}
}
cout << (dp[n-1]==MAX ? -1 : dp[n-1]);
}
11660 구간 합 구하기 5
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
| 시간 제한 | 입력 | 범위 |
| 1초 | N, M, i, j | 1 ≤ N ≤ 100,000 // 1 ≤ M ≤ 100,000 // 1 ≤ i ≤ j ≤ N |
NxN 크기의 표에서 (x1, y1)부터 (x2, y2)까지의 합을 출력하라.
접근법
누적 합을 이용하고, 경계를 잘 구분하면 금방 풀 수 있는 문제이다.
배열의 값을 입력받을 때, dp 배열의 동일한 인덱스에 (1, 1)부터 해당 칸까지의 누적값으로 저장한다.
(편한 설명을 위하여 인덱스가 1부터라고 가정한다.)
주어진 구간의 합을 구하는 방법
큰 구간에서 윗 구간과 왼쪽 구간을 빼고 공통 부분(중복 제거된 부분)을 다시 더해준다.
예시 4x4 크기 표에서 (2, 2)부터 (3, 4)까지 합 구하기
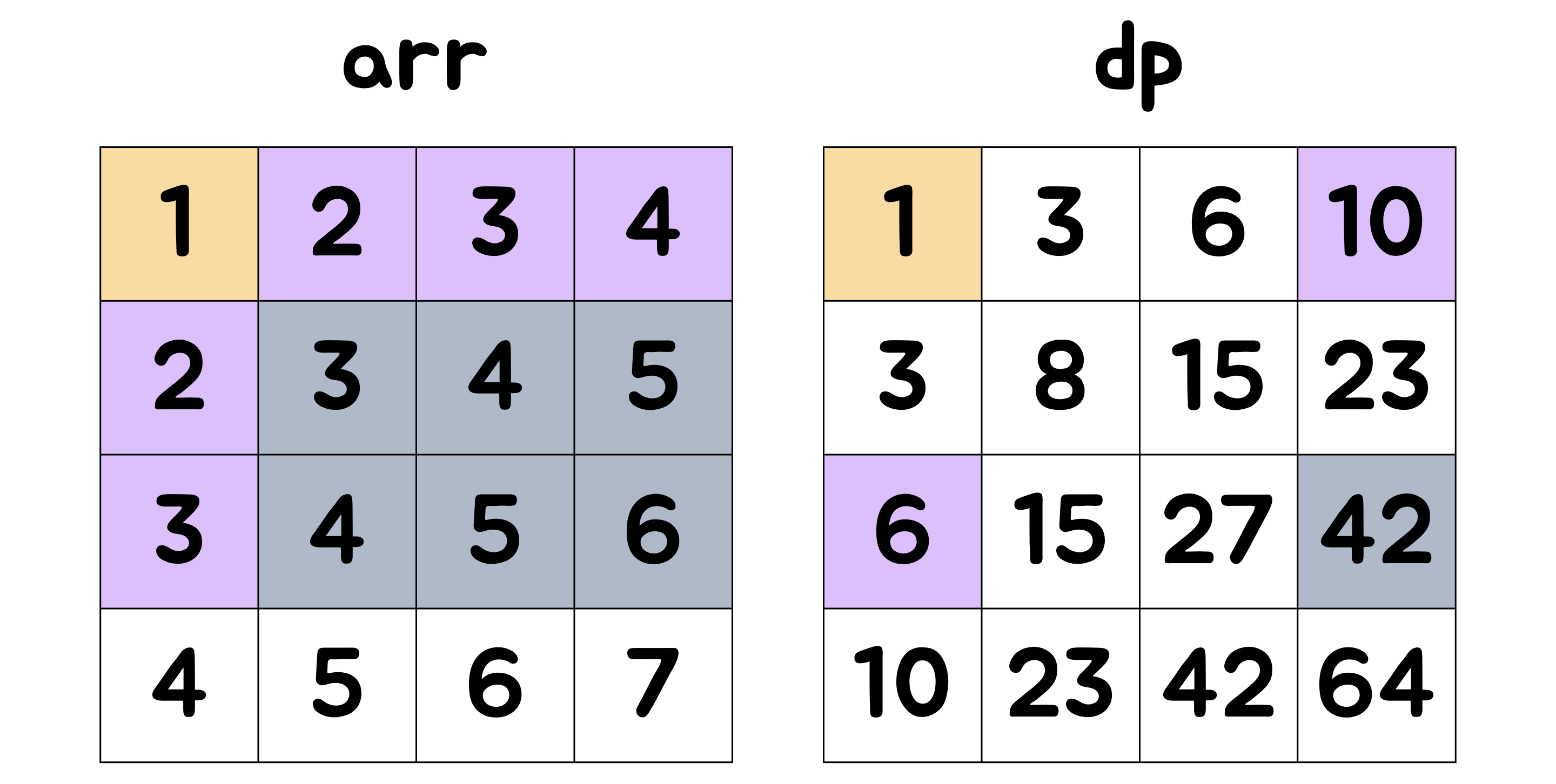
N=4가 주어졌을 때, 원래 배열은 왼쪽 표와 같으며, 이 때 dp 배열은 오른쪽 표와 같다.

(2, 2)부터 (3, 4)까지의 합을 구하라고 했을 때, 이는 아래 붉은 구간의 값을 합하는 것과 같다.
이 때, 큰 구간은 dp[3][4]에 해당하며 이는 아래 어두운 구간의 합을 의미한다.
dp[3][4] = 1 + 2 + 3 + 4 + 2 + 3 + 4 + 5 + 3 + 4 + 5 + 6 = 42

dp[3][4]은 arr[1][1]부터 arr[3][4]까지의 모든 값을 합한 값이 저장되어있다.
따라서, 일부를 제외해야 한다.
위에서 적어둔 '윗 구간과 왼쪽 구간을 빼고 공통 부분(중복 제거된 부분)을 다시 더해준다.'가 여기에 속한다.
글자의 색과 아래 그림의 색을 연결하여 생각해 보자.
arr[1][1]부터 arr[3][4] 중에서, 구간 (2, 2)부터 (3, 4)까지의 합을 구하기 위해서
arr[1][1], arr[1][2], arr[1][3], arr[1][4] / arr[2][1], arr[3][1], arr[4][1] 값은 필요 없다.
필요 없는 부분을 보라색으로 칠해보면 아래와 같다.
이는 또한 dp 배열의 값으로 표현할 수 있는데, 각각 dp[1][4]와 dp[4][1]에 해당한다.
하지만,
두 값을 dp[3][4]에서 모두 빼면, 중복해서 제외되는 구간이 존재한다. 이는 다시 더해주어야 한다.
해당 예제에서 이 부분은 주황색 구간, 즉, dp[1][1]과 같다.

따라서, 구간 (2, 2) ~ (3, 4)의 합을 구하는 식은 다음과 같다.
dp[3][4] - dp[1][4] - dp[3][1] + dp[1][1]
이를 일반화 하면 다음과 같다.
점화식
(x1, y1) ~ (x2, y2)의 합 = dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1]
제출
맞았습니다!!
Code - C++
코드를 보기 전에 스스로 구현해 보는 것을 권장합니다.
#include <iostream>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int n, m, temp;
cin >> n >> m;
int dp[n+1][n+1];
for(int i=0; i<=n; i++){
dp[0][i] = 0;
dp[i][0] = 0;
}
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
cin >> temp;
dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + temp;
}
}
int x1, y1, x2, y2, ans;
for(int i=0; i<m; i++){
cin >> x1 >> y1 >> x2 >> y2;
ans = dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1];
cout << ans << "\n";
}
}
